[논문 리뷰] Deformable Convolutional Networks

오늘 리뷰할 논문의 제목은 Deformable Convolutional Networks 입니다. ICCV 2017에서 제안된 논문이며, Convolution filter의 고정된 field를 offset이라는 개념을 통해 유기적으로 변화할 수 있도록 하였습니다.

 

https://arxiv.org/pdf/1703.06211.pdf

 

 

기존의 CNN은 몇가지 한계가 있었습니다. 가장 큰 이유는 CNN이 본질적으로 기하학적인 구조(크기, 모양 등)가 고정되어있다는 것입니다. 이 때문에 일반화가 잘 되지 않고 복잡한 Translation에 대한 성능이 낮았습니다.

 

저자는 보통 우리가 시각적으로 볼 때 객체의 크기나 위치 등이 고정되어 있지 않기 때문에 CNN의 수용필드가 변화하는 것이 더 좋은 성능을 낼수 있다고 생각했습니다. 그래서 offset을 통해 수용필드를 유기적으로 변화시킬수 있는 방법을 제안했습니다. 바로 Deformable Convolution과 Deformable Roi Pooling 입니다. 이 두 모듈은 심지어 가벼워서 학습하는데 큰 parameter가 들지 않습니다.

 

 

Deformable Convolutional Networks

보통의 이미지는 (H x W x C)의 3차원(3D)으로 이루어져있지만 DCN의 Offset 2차원(2D) 도메인으로 이루어져있습니다. 즉 Channel 마다 다른 Offset을 적용하지는 않습니다. 여기서 Offset은 DCN이 Deformable Convolution을 할 때 filter의 위치를 나타내는 Guide Line이라 할 수 있습니다. 물론 3D로 확장도 가능합니다.

 

 

Deformable Convolution

 Convolution은 2가지 단계를 거칩니다.

1. featuremap $x$에 대해 grid(filter) $\mathcal{R}$을 사용해 샘플링.

2. 샘플링 된 값에 대해 weight $w$를 사용해 계산

 

여기서 grid $mathcal{R}$은 다음과 같이 정의됩니다. (3x3 Convolution)

$\mathcal{R}=\{(-1,-1),(-1,0),...,(0,1),(1,1)\}$

 

이때  Convolution 하는 위치인 $p_0$에 대한 연산을 수행해 feature map $y$를 얻을 수 있습니다.

 

$y(p_0)=\sum_{p_n\in\mathcal{R}}^{}w(p_n)\cdot x(p_0+p_n)  \tag{1}$

 

deformable convolution의 경우 $\mathcal{R}$은 offset $\{ \Delta p_n | n=1,...,N \}$를 추가하여 연산합니다.

이때 $N=| \mathcal{R} |$입니다. 만약 3 x 3 filter를 사용한다면 N=9라는 뜻입니다. Deformable Convolution의 feature map $y$는 다음과 같이 정의할 수 있습니다.

 

$y(p_0)= \sum_{p_n \in \mathcal{R}}^{} w(p_n) \cdot x(p_0+p_n+\Delta p_n) \tag{2}$

 

위 식을 보면 가운데 점인 $p_0$의 주변 field의 위치 정보 이외에도 $p_n$에 대한 offset field의 값을 추가로 가져옵니다. 즉 convolution의 각 filter의 위치가 $\Delta p_n$만큼 자유롭게 움직이게 됩니다. 이때 $\Delta p_0$의 값은 소수점의 미세한 값입니다.

 

소수점의 값을 가지기 떼문에 실질적으로 이미지의 pixel과 pixel 사이의 값을 연산에서 사용하게 됩니다. 사실 디지털로 이루어진 픽셀 사이의 소수점 값은 존재하지 않기 때문에 저자는 픽셀간 bilinear interpolation(선형 보간법)으로 해결했습니다.

 

$x(p) = \sum_{q}^{} G(q,p) \cdot x(q) \tag{3}$

 

p는 2번식에서 나온 $p_0+p_n+\Delta p_n$ 값, 즉 소수점으로 이루어진 가상의 점입니다. 반면 q는 p가 위치하는 공간의 모든 점의 집합입니다. $G( \cdot , \cdot )$은 bilinear interpolation kernel입니다. G는 2차원 이미지에 대해 대응하게 되므로 $x$와 $y$에 대한 계산을 통해 이루어집니다.

 

$G(q, p)=g(q_{x}, p_{x}) \cdot g(q_{y}, p_{y}) \tag{4}$

 

위식은 $g(a, b) = max(0, 1-|a-b|)$를 따릅니다. 3, 4번 식을 통해 DCN의 역전파가 이루어집니다. 

 

위의 그림을 보면 offset field는 input에 대한 Convolution 연산을 통해 진행되는데  Cannel의 수가 2N개입니다. 이것은 2차원 이미지여서 그렇습니다. 가로축과 세로축에 대한 $\Delta p_n$값이 필요하기 때문입니다. 앞서 N은 kernel의 크기라 했으므로 좌표의 개수 x kernel의 크기 = 2N입니다. 만약 3차원이라면 3N이 될 것입니다.

 

Deformable RoI Pooling

 

 

Deformable RoI Pooling을 알기위해서는 RoI Pooling에 대한 사전지식이 있어야 합니다.

 

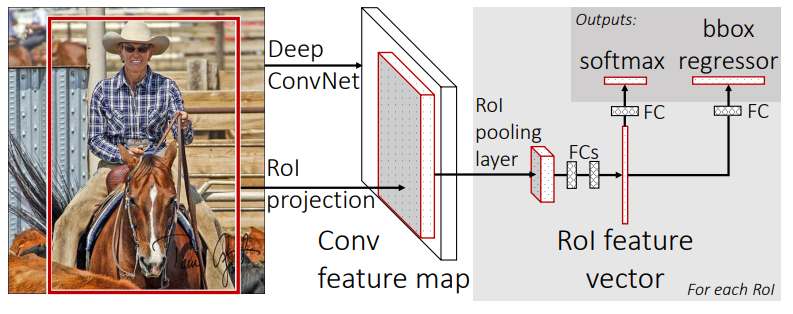
RoI Pooling은 Fast R-CNN에서 제안되었습니다. Fast R-CNN에서 RoI Projection 된 output 값은 크기가 제각각인데 이는 고정된 크기의 입력을 필요로 하는 Fully Connected Layer에 사용할수가 없습니다. 여기서 output 값을 FC Layer에 입력할 수 있도록 고정된 크기로 변경하는 layer가 RoI Pooling Layer입니다. 

 

 

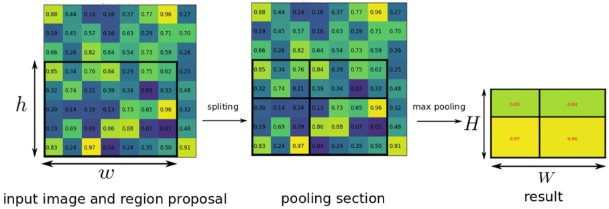
위 이미지는 RoI Pooling을 설명하는데 가장 많이 사용하는 그림입니다. 살짝 헷갈릴 수 있는데 $h \times w$의 크기로 projection된 값에 대해서 bin으로 grid를 나누어줍니다. bin이란 fc layer에서 사용할 수 있도록 만들 크기의 단위입니다. 즉 $H \times W$의 값 = bin의 개수 라 할수 있습니다. grid로 나눈 각 bin은 Max Pooling을 통해 $H \times W$크기를 가진 pooling featuremap으로 변환됩니다.

 

참고로 DCN에서는 bin의 수($H \times W$)를 $k \times k$개로 생각합니다. $(i, j)$번째 bin에 대한 RoI Pooling 연산을 수식으로 나타내보면 다음과 같습니다.

 

$y(i, j) = \sum_{p \in bin(i,j)}^{} x(p_0+p) / n_{ij} \tag{5}$

 

$n_{ij}$는 bin에 있는 pixel의 개수입니다. Deformable RoI pooling은 offsets $\{ \Delta p_{ij} | 0 \leq i, j < k \} $ 가 추가됩니다. 

 

$y(i, j) = \sum_{p \in bin(i, j)}^{} x(p_0 + p + \Delta p_{ij}) / n_{ij} \tag{6}$

 

Deformable RoI Pooling은 2번식 Deformable Convolution과 큰 차이는 없습니다. $n_{ij}$로 계속 나누는 이유는 아마 average pooling을 사용하는 것을 표현한 것 같습니다. Fast R-CNN에서는 max pooling을 하지만 DCN에서는 max pooling에 대한 내용이 아예 나오지 않습니다. 아무래도 R-FCN에서 average pooling을 사용하던  max pooling을 사용하던 딱히 상관없어 average pooling을 사용했는데 본 논문에도 동일하게 average pooling을 사용한 것 같습니다.

또한 여기서는 offset을 추출할 때 FC Layer를 사용합니다. 이유는 딱히 논문에 언급되어있지는 않습니다.

 

Position-Sensitive (PS) RoI Pooling

PS RoI Pooling은 R-FCN에서 제안한 새로운 RoI Pooling으로 각 Position에 대한 부분을 개별적으로 봅니다. 또한 RoI Projection이나 pooling 이후 나오는 연산들 없이도 좋은 성능을 발휘할 수 있는 Pooling입니다. $k \times k$는 이전과 마찬가지로 offset의 크기를 나타내며 C는 Object의 Class 개수를 뜻합니다.

 

 

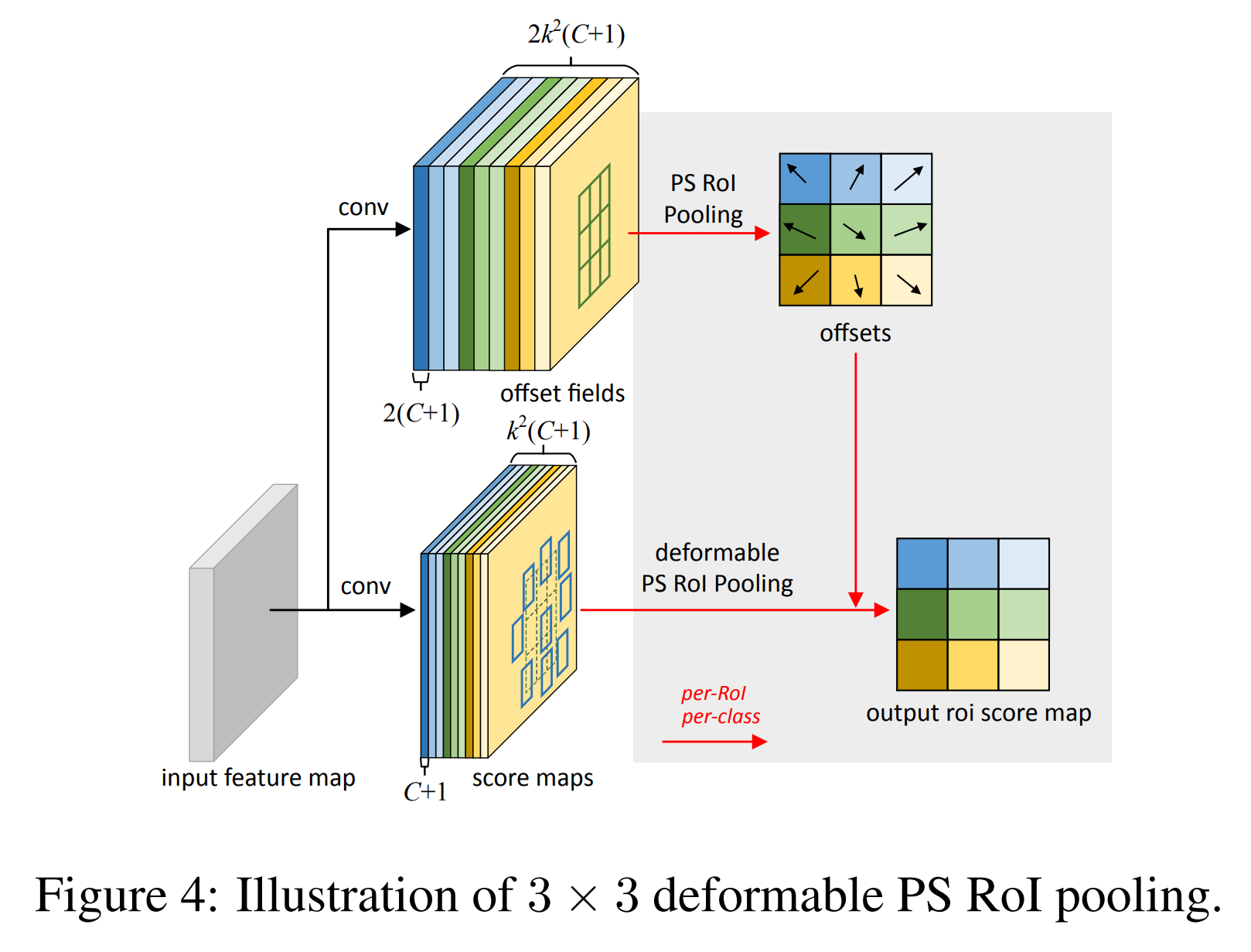
Deformable PS RoI Pooling은 offset을 추출할 때 다시 Convolution을 사용합니다. 6번 수식과 다른점은 각 Position에 대한 Feature map channel이 정해져있기 때문에 $x$가 아닌 $x_{i,j}$를 사용한다는 것입니다.