[논문 리뷰] StyTr²: Image Style Transfer with Transformers
- -
오늘 리뷰할 논문은 CVPR 2022에서 발표한 StyTr² 입니다.
https://arxiv.org/abs/2105.14576
StyTr$^2$: Image Style Transfer with Transformers
The goal of image style transfer is to render an image with artistic features guided by a style reference while maintaining the original content. Owing to the locality in convolutional neural networks (CNNs), extracting and maintaining the global informati
arxiv.org
Style Transfer는 원본의 Content를 유지하면서 Style Reference를 이미지에 렌더링하는 것입니다. 초기의 Texture 합성을 기반으로 하는 기존의 Style Transfer는 선명한 Style 이미지를 생성할 수 있지만, 계산이 매우 복잡했습니다.
이후 CNN을 기반으로 하는 Style Transfer가 대두되었습니다. 그러나 CNN을 기반으로 하는 Style Transfer 방식은 Style과 Contents 사이의 관계를 모델링 하는 능력이 제한되어 있기 때문에 항상 만족스러운 결과를 얻기 어렵습니다.
또한 CNN은 local한 특성을 가지고 있기 때문에 Global Information을 추출하기 어렵습니다. 이를 해결하기 위해서는 충분히 Layer를 쌓아야 하는데 CNN Layer를 계속 쌓게 되면 해상도나 여러 Information이 손상됩니다. 또한 최근 연구에 따르면 아래 그림과 같이 CNN 기반의 Style Transfer 작업은 Contents가 손상되는 모습을 볼 수 있었습니다.

최근 자연어 처리에서 Transformer가 대두되고 난 뒤 Transformer 기반 아키텍처가 Vision Process에서도 사용되고 있습니다. Transformer는 두가지 이점을 가지고 있는데, 먼저 Self-Attention을 통해 Global Information을 자유롭게 학습할수 있습니다. 두번째로 Transformer 구조는 입력에 대한 관계를 모델링하고, 각각의 Layer는 유사한 구조에 대한 정보를 추출할 수 있습니다. 즉 Transformer는 세부적인 정보가 누락되지 않는 강력한 Repregentation 성능을 가지고 있습니다.
따라서 저자는 Transformer를 기반으로하는 StyTr²를 제안합니다. StyTr²는 Contents, Style에 대한 2가지 Transformer Encoder를 사용하며, Transformer Decoder를 통해 점진적으로 Sequence를 뽑아냅니다. StyTr²는 NLP의 Transformer와 2가지의 다른점을 가지고 있는데, 이는 다음과 같습니다:
- NLP의 문장 Sequence와 달리, image에 대한 Sequence Token은 Contents Information에 연관되어 있습니다.
- Style Transfer 작업 시 다양한 해상도에서 스타일을 바꾸는 것을 목표로 합니다. 다양한 해상도는 Positinal Encoding이 계속 바뀌게 되어 품질이 저하됩니다. 따라서 일반적으로는 이미지의 Resolution을 고정하여 학습하지만, 영상의 Semantic Feature와 동적인 Resolution을 바탕으로 하는 Content aware Positional Encoding scheme(CAPE)를 사용합니다.
또한 논문의 Contribution은 다음과 같습니다.
- Transformer를 기반으로하는 StyTr²를 제안합니다.
- 여러 Resolution에서도 대응가능한 Style Transfer에 최적화된 CAPE를 제안합니다.
- StyTr²가 이전보다 더 뛰어난 성능을 보여주는것을 실험을 통해 증명합니다.
StyTr²
Transformer가 Style Transfer에서 feature의 Long-range Dependencies를 잘 포착시키기 위해 저자는 Sequential한 patch를 생성하였습니다. $I_C \in \mathbb{R}^{H \times W \times 3}$의 크기를 가진 Contents Image와 $I_S \in \mathbb{R}^{H \times W \times 3}$의 크기를 가진 Style Image에 대해서 patch로 쪼갠뒤 Linear Projection을 통해 Feature Embedding $\varepsilon$을 생성합니다.
$\varepsilon$은 $L \times C$의 크기를 가졌고, 이때 $L ={{H \times W} \over {m \times m}}$입니다. m은 patch size이며 8을 사용하였습니다.

Content-Aware Positional Encoding (CAPE)
Transformer based model을 사용할 경우 Positional Encoding이 필수적입니다. i, j번째 patch에 대한 Attention Score는 다음과 같이 계산됩니다.
$A_{i, j}=((\varepsilon_{i}+\mathcal{P}_{i})W_{q})^{T}((\varepsilon_{j}+\mathcal{P}_{j})W_{k}) =W_{q}^{T}\varepsilon_{i}^{T}\varepsilon_{j}W_{k}+W_{q}^{T}\varepsilon_{i}^{T}\mathcal{P}_{j}W_{k}+W_{q}^{T}\mathcal{P}_{i}^{T}\varepsilon_{j}W_{k}+W_{q}^{T}\mathcal{P}_{i}^{T}\mathcal{P}_{j}W_{k}, \tag{1}$
$W_{q}$ 와 $W_{k}$는 각각 query와 key에대한 parameter이며 $\mathcal{P}_{i}$는 i번째 1차원 Positional Encoding을 의미합니다. 2D일 경우, 패치의 Pixel $(x_{i}, y_{i})$와 $(x_{j}, y_{j})$의 위치 관계는 다음과 같이 나타낼 수 있습니다:
$\mathcal{P}(x_{i}, y_{i})^{T}\mathcal{P}(x_{j}, y_{j})=\sum\limits_{k=0}^{{{d}\over{4}}-1}[cos(w_{k}(x_{j}-x_{i})+cos(w_{k}(y_{j}-y_{i}))], \tag{2}$

$w_{k}=1/10000^{2k/128}, d=512$입니다.
저자는 기존의 Positional Encoding에 대해서 2가지 의문점을 제시했습니다.
- 이미지 생성 분야에서 영상의 의미론적인 정보에 대한 Positional Encoding을 계산해야 할까요? 두개의 patch들은 공간적인 정보만을 가지고 관계를 형성합니다. 위의 그림에서 붉은 색 patch와 초록색 patch 사이의 distance보다 붉은색 patch와 시안색 patch 사이의 거리가 멀어야 합니다. (일반적인 거리의 관점이 아니라 embedding vector가 좀더 비슷해야 한다는 의미 같습니다.) 즉 의미론적인 부분을 따지는 NLP의 Positional Encoding은 잘 맞지 않을 수 있습니다.
- 입력 영상의 크기가 매우 클때도 여전히 sin과 cos을 사용하는 Positional Encoding이 Vison Task에서 잘 동작할까요? 위의 그림에서 크기를 키웠을 때와 키우지 않았을 때 배의 같은 위치에 대해 patch의 상대적인 거리가 매우 변화합니다. 따라서 Vison Task의 여러 Resolution에 대해서는 맞지 않습니다.
따라서 저자는 Scale의 영향을 받지 않고 Style Transfer에 더 적합한 Content-Aware Positional Encoding(CAPE)를 제안했습니다. patch의 상대적 거리를 고려하는 일반적인 Positional Encoding과 달리 CAPE는 영상 Content의 semantics(의미)를 기준으로 합니다. $I \in \mathbb{R}^{H \times W \times 3}$인 Image에 대하여 $n \times n$ CAPE에 대한 수식은 다음과 같습니다:
$\mathcal{P_{L}}=\mathcal{F}_{pos}(AvgPool_{n \times n}(\varepsilon)) \\ \mathcal{P_{CA}}(x,y) = \sum\limits_{k=0}^{s}\sum\limits_{l=0}^{s}(a_{kl}\mathcal{P_{L}}(x_{k}, y_{l})), \tag{3}$
$\mathcal{P_{L}}$은 $\varepsilon$에 대한 학습 가능한 Positional Encoding입니다. 이때 Sequence(Feature Embedding)인 $\varepsilon$은 Average Pooling한뒤 1x1 Convolution인 $\mathcal{F}_{pos}$를 통과합니다. n은 실험을 통해 18이라는 값을 사용하였고, $a_{kl}$은 보간된 weight, s는 positional encoding 중인 patch의 주변 neighbor patch들의 수를 의미합니다. 즉 pixel $(x,y)$에 대하여, CAPE는 patch의 주변 patch에 대한 information을 통해 결정되게 됩니다.
Style Transfer Transformer
Transformer Encoder
저자는 Long-range Dependency를 위해 Transformer 기반의 모델링을 했다고 앞서 언급했습니다. 다른 Vison task와는 다르게 Style Transfer는 Content와 Style에 대한 서로 다른 Domain Input을 필요로 합니다. 따라서 두가지 domain에 대한 feature를 뽑아낼 수 있도록 2가지 Transformer Encoder를 사용합니다.
이번에는 기존 Transformer를 수식으로 나타내보겠습니다. (Content c에 대한 Encoder는 기존 Transformer Encoder와 유사하기 때문입니다.)
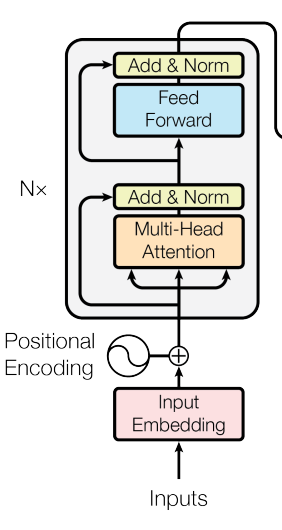
Positional Encoding이 완료된 Content sequence인 $Z_{c} = \{ \varepsilon_{c1} + \mathcal{P_{CA1}}, \varepsilon_{c2} + \mathcal{P_{CA2}}, ..., \varepsilon_{cL} + \mathcal{P}_{\mathcal{CA}L} \} $는 Transformer의 Encoder에 입력됩니다. 이 때 Encoder는 multi-head self-attention(MHSA)과 feed-forward network(FFN)을 포함하고 있습니다. input sequence에 대한 Query, Key, Value는 다음과 같습니다:
$Q=Z_{c}W_{q}, K=Z_{c}W_{k}, V=Z_{c}W_{v}, \tag{4}$
$W_{q}, W_{k}, W_{v} \in \mathbb{R}^{CF \times d_{head}}$입니다.MHSA는 다음과 같이 적용됩니다. (기존 논문과 마찬가지로 multi-head self-attention을 MHSA으로 표기하였습니다.)
$\mathcal{F}_{MHSA}(Q,K,V)=Concat(Attention_{1}(Q,K,V), ..., Attention_{N}(Q, K, V))W_{o}, \tag{5}$
$W_{o} \in \mathbb{R}^{C \times C}$는 학습가능한 parameter입니다. N은 $d_{head}={C \over N}$인 attention head의 개수입니다.이후 MHSA 및 FFN 이후 추가되는 Residual Connection은 다음과 같이 정의됩니다.
$Y'_{c}=\mathcal{F}_{MHSA}(Q,K,V)+Q, \\ Y_{c}=\mathcal{F}_{FFN}(Y'_{c})+Y'_{c}, \tag{6}$
Feed Forward Network $\mathcal{F}_{FFN}(Y'_{c})=max(0, Y'_{c}W_{1}+b_{1})W_{2}+b_{2}$입니다. Layer Normalization은 이후에 한번 적용합니다.
이번에는 Style sequence에 대한 Encoder를 살펴보겠습니다. Input Style Sequence인 $Z_{s}= \{\varepsilon_{s1},\varepsilon_{s2},...,\varepsilon_{sL} \}$는 $Y_{s}$로 인코딩 되는데, Content와 비슷한 흐름으로 연산되지만 Positional Encoding을 하지 않습니다. Style Sequence의 위치 정보는 입력 및 출력될 Style Information에 필요하지 않기 때문입니다.
Transformer Decoder
Transformer Decoder는 $Y_{c}$를 $Y_{s}$에 따라 회귀 변환하도록 학습합니다. NLP와 다르게 입력은 모든 patch에 대하여 초기에 한번만 합니다. 각 Decoder는 2개의 MHSA과 1개의 FFN를 사용합니다. 입력은 encoded content sequence $\hat{Y_{c}}=\{ Y_{c1}+\mathcal{P_{CA1}}, Y_{c2}+\mathcal{P_{CA2}},..., Y_{cL}+\mathcal{P}_{\mathcal{CA}L} \},$(이때도 마찬가지로 Positional Encoding을 합니다.)와 style sequence $Y_{s}=\{ Y_{s1}, Y_{s2}, ..., Y_{sL} \}$입니다. 이 때 content sequence는 Query, style sequence는 Key와 Value로 사용합니다:
$Q=\hat{Y}_{c}W_{q}, \\ K=Y_{s}W_{k}m, \\ V=Y_{s}W_{v}, \tag{7}$
output sequence X는 다음 수식을 통해 만들어 집니다:
$X''=\mathcal{F}_{MSA}(Q,K,V)+Q, \\ X'=\mathcal{F}_{MSA}(X''+\mathcal{P_{CA}},K,V)+X'', \\ X=\mathcal{F}_{FFN}(X')+X', \tag{8}$
마지막으로 Encoder와 마찬가지로 LN을 사용합니다.
CNN Decoder
${{HW} \over {64}} \times C$ 크기의 output sequence인 X는 바로 upsampling 하지 않고 3개의 CNN 기반 Decoder Layer를 통과합니다. 각 layer는 $3 \times 3 Conv+ReLU+Upsample \times 2$로 이루어져 있습니다. Layer를 모두 지나면 다시 $H \times W \times 3$의 resolution을 가진 이미지로 변환됩니다.
Network optimization
StyTr²는 Output Image인 $I_{o}$와 Content Image $I_{C}$, $I_{o}$와 $I_{s}$에 대하여 각각 Perceptual Loss를 적용합니다. 의외로 Transformer를 기반으로 하지 않고 전통적인 방식인 VGG based model로 loss를 산출해 냅니다.
$\mathcal{L}_{c} = {{1} \over {N_{l}}} \sum\limits_{i=0}^{N_l}||\phi_{i}(I_{o})-\phi_{i}(I_{c})||_{2} \tag{9}$
$\mathcal{L}_{s} = {{1} \over {N_{l}}} \sum\limits_{i=0}^{N_{l}}||\mu(\phi_{i}(I_{o}))-\mu(\phi_{i}(I_{s}))||_{2} + ||\sigma(\phi_{i}(I_{o}))-\sigma(\phi_{i}(I_{s}))||_{2} \tag{10}$
$\mu(\cdot)$와 $\sigma(\cdot)$은 각각 평균과 분산입니다.
저자는 이외에도 Identity Loss를 추가했습니다. Identity Loss는 입력에 아무 변화가 없을 때 결과 이미지가 그대로 나오는지에 대한 Loss 입니다. Style Transfer 같은 경우에는 Content, Style에 각각 동일한 입력을 했을 때 입력과 출력이 같은지를 봐야 합니다. 입력 $I_{c}(I_{s})$에 대한 출력이 $I_{cc}(I_{ss})$ 일때 identity Loss는 다음과 같습니다:
$\mathcal{L}_{id1} = ||I_{cc}-I_{c}||_{2} + ||I_{ss}-I_{s}||_{2}, \\ \mathcal{L}_{id2} = {{1} \over {N_{l}}} \sum\limits_{i=0}^{N_l}||\phi_{i}(I_{cc})-\phi_{i}(I_{c})||_{2}+||\phi_{i}(I_{ss})-\phi_{i}(I_{s})||_{2} \tag{11}$
$\mathcal{L}_{id2}$를 보면 identity에 대한 perceptual Loss도 사용하는 것을 볼 수 있습니다. 결과적으로 minimize 해야 하는 전체 Loss function은 다음과 같습니다:
$\mathcal{L} = \lambda_{c}\mathcal{L}_{c}+\lambda_{s}\mathcal{L}_{s}+\lambda_{id1}\mathcal{L}_{id1}+\lambda_{id2}\mathcal{L}_{id2}, \tag{12}$
$\lambda$는 하이퍼파라미터로 $\lambda_{c}, \lambda_{s}, \lambda_{id1}, \lambda_{id2}$ 순서대로 10, 7, 50, 1의 값을 할당해 주었습니다.
Experiments
Qualitative Evaluation

시각적으로 봤을 때 다른 방식에 비해 좀더 자연스럽고 좋은 성능을 가졌음을 알수 있습니다.
Quantitative Evaluation

Content와 Style에 대한 Perceptual Loss를 비교하였을때, Content는 여러 모델들 사이에서 가장 낮았으며, Style은 2번째로 낮았습니다. Content와 Style모두 벨런스 있게 좋은 성능을 보여주었습니다.
Analysis of Content Leak
CNN-based 모델들은 image의 content에 대한 디테일을 잘 추출하지 못해서 Content Leak(Content 누출)가 일어나는 경향이 있습니다. Content Leak는 Style Transfer 시 이미지의 Content가 뭉게지거나 이에대한 특징이 잘 나타나지 않게 되는 현상입니다. Content Leak는 Style Transfer 한 이미지를 재귀적으로 Style Transfer를 적용하면 시각적으로 발견하기 쉽습니다. 다음 수식을 보시면 이해하기 쉽습니다.
$I_{o}^{i}=G_{i}(...(G_{2}(G_{1}(I_{c}, I_{s}),I_{s})...,I_{s}), \tag{13}$

style Transfer를 20번 적용했을 때, 대부분의 모델은 Content Leak가 일어났지만, StyTr²는 큰 변화가 없음을 확인할 수 있습니다.
Analysis of CAPE
저자는 512 x 512, 256 x 256 Resolution의 이미지에 대한 Sinusoidal Positional Encoding과 CAPE를 비교했습니다.

CAPE의 결과가 더 좋은 모습을 확인 할 수 있습니다. 특히 Style 은 Positional Encoding을 하지 않아서 그런지 Style 이 골고루 위치하는 모습을 보였습니다.
'Generative Models' 카테고리의 다른 글
| [논문 리뷰] Animate Anyone (0) | 2024.03.17 |
|---|---|
| 생성 모델 논문 추천 List - Generative Adversarial Networks (2) | 2023.12.11 |
| [논문 리뷰] Understanding Diffusion Models: A Unified Perspective (3) (0) | 2023.12.11 |
| [논문 리뷰] Understanding Diffusion Models: A Unified Perspective (2) (4) | 2023.08.12 |
| [논문 리뷰] Understanding Diffusion Models: A Unified Perspective (1) (0) | 2023.07.06 |
당신이 좋아할만한 콘텐츠
소중한 공감 감사합니다