[논문 리뷰] Understanding Diffusion Models: A Unified Perspective (1)
- -
Understanding Diffusion Models: A Unified Perspective는 Google Brain에서 Diffusion model에 대한 이해를 돕기위해 만든 논문입니다. 이번 기회에 Diffusion model을 이해하기 위한 여러 수식이나 정의를 정리해 보려 합니다.
먼저 이번 포스팅에서는 Diffusion model 이전에 나온 Variational Auto Encoder 관련 수식을 정리합니다. 이때 나오게 되는 수식들은 Diffusion model과 상당히 연관성이 있습니다.
Evidence Lower Bound (ELBO)
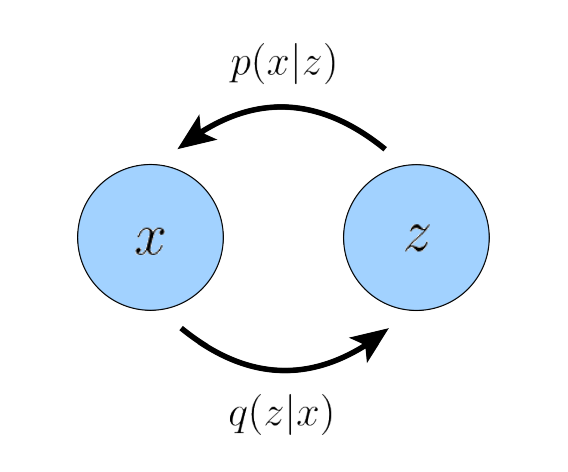
우리과 관측한 data인 x와 latent variable(잠재 변수) z에 대해서 결합확률 분포인 $p(x, z)$를 생각할 수 있습니다. Likelihood Based(가능도 기반) 방식의 생성모델들의 목적은 모든 관측값 x에 대해 likelihood가 최대가 되는 p(x)를 찾는것입니다. p(x)와 잠재변수에 대한 p(x, z)가 일치하게되면 결국 관측값들과 정확히 일치하는 데이터를 생성할 수 있기 때문입니다. 즉 다음과 같은 수식이되도록 모델을 학습시킵니다:
$$p(x) = \int {p(x,z) dz} \tag{1}$$
확률 (probability)에 대한 chain rule에 의해 p(x)는 다음과 같이 정리할 수도 있습니다:
$$p(x) = {{p(x, z)} \over {p(z|x)}} \tag{2}$$
먼저 각 Component를 정의해보겠습니다.
$p(\cdot)$: $\cdot$에 대한 확률을 의미합니다. 예를 들면 $p(x)$는 관측된 x에 대한 likelihood를 의미하며 $p(x,z)$는관측된 x와 latent variable z가 동시에 일어날 확률을 의미합니다.
$q_\phi(\cdot)$: $\phi$를 파라미터로 가지는 근사 확률입니다. 즉 $\phi$를 통해 학습가능한 신경망이 근사할 확률을 의미합니다.
Likelihood란?
Likelihood(가능도, 우도)는 관측값x가 임의의 확률분포 D에서 관측되었을 확률을 의미합니다. 즉 분포 D에 대해서 x가 D의 평균에 가까울수록 Likeliyhood의 값이 높습니다. 여기서 Likelihood를 최대화 한다는 것(Maximum Likelihood)은 모든 관측값의 가능도가 최대가 되는 값을 의미합니다. 관측값에 대한 가능도의 곱이 최대가 될때 Maximum Likelihood라고 합니다.
자세한 내용은 아래 블로그에 잘 설명되어있으니 참조하세요.
https://jjangjjong.tistory.com/41
확률(probability)과 가능도(likelihood) 그리고 최대우도추정(likelihood maximization)
* 우선 본 글은 유투브 채널StatQuest with Josh Starmer 님의 자료를 한글로 정리한 것 입니다. 만약 영어듣기가 되신다면 아래 링크에서 직접 보시는 것을 추천드립니다. 이렇게 깔끔하게 설명한 자료
jjangjjong.tistory.com
Probability Chain Rule
Probability Chain Rule은 이산/연속확률 분포 X와 Y에 대해 다음이 성립하는 것을 의미합니다.
- $X=x$로 주어진 확률변수 $Y$의 조건부 분포는
$$f(y|x) = {{f(x,y)} \over {f_{X}(x)}}$$
- $Y=y$로 주어진 확률변수 $X$의 조건부 분포는
$$f(x|y) = {{f(x,y)} \over {f_{Y}(y)}}$$
참고로 조건부 분포 $p(x|y)$는 p x given y라고 읽습니다.
말을 쉽지만, p(x)에 대한 Maximum Likelihood를 찾는것은 굉장히 어려운 일입니다. 그렇지만 위의 2가지 식을 통해 우리는 Evidence Lower Bound(ELBO)를 찾을수 있습니다. Evidence란 p(x)를 의미함으로, p(x)에 대한 하한을 z에 대한 공식으로 만들수 있습니다. 우리가 만약 ELBO를 최대화 하면 p(x)의 하한이 커지기 때문에 자연스렵게 p(x)를 최대화 할수 있다는 것이 ELBO의 이론입니다.
$$\mathbb{E}_{q_{\phi}(z|x)} \bigg[log{{p(x,z)} \over {q_{\phi}(z|x)}}\bigg] \tag{3}$$
$$log\ p(x) \ge \mathbb{E}_{q_{\phi}(z|x)} \bigg[log{{p(x,z)} \over {q_{\phi}(z|x)}}\bigg] \tag{4}$$
ELBO에 대한 방정식은 위와 같은데, 이제 ELBO에 대한 방정식을 유도해봅시다:
$$\begin{align}
log\ p(x) &= log \int{p(x, z)dz} \tag{5}
\\
&=log \int{{{p(x,z)q_{\phi}(z|x)} \over {q_{\phi}(z|x)}}dz} \tag{6}
\\
&=log \ \mathbb{E}_{q_{\phi}(z|x)} \bigg[ {{p(x,z)} \over {q_{\phi}(z|x)}} \bigg] \tag{7}
\\
&\ge \mathbb{E}_{q_{\phi}(z|x)} \bigg[log{{p(x,z)} \over {q_{\phi}(z|x)}}\bigg] \tag{8}
\end{align}$$
각 수식을 차근차근 뜯어봅시다.
먼저 Eq 5는 Eq 1에 log를 취한 형태입니다.
Eq 6은 ${{q_{\phi}(z|x)} \over {q_{\phi}(z|x)}} = 1$이기 때문에 우변에 값을 곱해주었습니다.
Eq 7은 기댓값(Expectation)에 대한 공식을 적용합니다.
Eq 8은 옌센 부등식(Jensen's Enquality)에 의해 함수 안쪽에 있는 log는 함수 바깥에 있는 log보다 작거나 같습니다.
Expectation
Expectation은 확률변수 X 대해 평균적으로 기대하는 값입니다. Expectation은 다음 공식을 따릅니다.
- 이산 확률 변수 X에 대한 Expectation:
$$E[X] = \sum_{i=1}^{n} {x_{i}p(x_{i})}$$
- 연속 확률 변수 X에 대한 Expectation:
$$E[X] = \int_{-\infty}^{\infty} {x\ p(x)dx}$$
만약 확률변수가 아닌 확률변수의 함수 $f(x)$에 대하여 Expectation을 구하면 다음과 같이 응용할 수 있습니다.
- 이산분포에 대하여 f(x)에 대한 Expectation:
$$E[f] = \sum_{x}{p(x)f(x)}$$
- 연속분포에 대하여 f(x)에 대한 Expectation:
$$E[f] = \int{p(x)f(x)dx}$$
이것을 ELBO에 역으로 적용하면 다음과 같은 공식을 얻을 수 있습니다: (사실 이게 맞는지 모르겠음..)
$$E_{q_{\phi}(z|x)}\bigg[{{p(x,z)} \over {q_{\phi}(z|x))}}\bigg] = \int {\bigg({{p(x,z)} \over {q_{\phi}(z|x))}}\bigg) q_{\phi}(z|x) dz}$$
Jensen’s Inequality
Jensen’s Inequality(옌센 부등식)에 대한 정의는 다음과 같습니다:
Expectation E(x)에 대하여 g(x)라는 Convex function(볼록 함수)는 다음이 성립합니다.
(g(x)의 2차미분이 존재하여야 함):
$$E \{ g(x) \} \ge g \{ E(x) \}$$
반대로 E(x)에 대하여 g(x)라는 Concave function(오목 함수)는 다음이 성립합니다:
$$E \{g(x)\} \le g \{ E(x) \}$$
볼록함수는 위로 볼록한 함수이며 반대로 오목함수는 아래로 볼록한 함수로 log 함수는 0 이상일 때 Concave function입니다. 따라서 log를 g(x)라 하면 다음 식이 성립합니다.
$$log \ \mathbb{E}_{q_{\phi}(z|x)} \bigg[ {{p(x,z)} \over {q_{\phi}(z|x)}} \bigg] \ge \mathbb{E}_{q_{\phi}(z|x)} \bigg[log{{p(x,z)} \over {q_{\phi}(z|x)}}\bigg]$$
우리는 Jensen's Inequality를 통해 ELBO를 유추할 수 있게 되었습니다. 그렇지만 이것만으로는 아직 ELBO를 최대화 하는 것에 대해 직관적으로 이해하기 힘듭니다. 따라서 위를 조금 변형해서 식을 새롭게 바꿔보겠습니다:
$$\begin{align}
\log{p(x)} &= log \ p(x) \int{q_{\phi}(z|x) dz} \tag{9}
\\
&= \int{q_{\phi}(z|x)(log\ p(x))dz} \tag{10}
\\
&=\mathbb{E}_{q_{\phi}(z|x)}[ log\ p(x) ] \tag{11}
\\
&= \mathbb{E}_{q_{\phi}(z|x)} \bigg[ log {{p(x, z)} \over {p(z|x)}} \bigg] \tag{12}
\\
&=\mathbb{E}_{q_{\phi}(z|x)} \bigg[ log {{p(x,z) q_{\phi}(z|x)} \over p(z|x) q_{\phi}(z|x)} \bigg] \tag{13}
\\
&=\mathbb{E}_{q_{\phi}(z|x)} \bigg[ log{{p(x,z)} \over {q_{\phi}(z|x)}} \bigg] + \mathbb{E}_{q_{\phi}(z|x)} \bigg[ log{{q_{\phi}(z|x)} \over {p(z|x)}} \bigg] \tag{14}
\\
&= \mathbb{E}_{q_{\phi}(z|x)} \bigg[ log{{p(x,z)} \over {q_{\phi}(z|x)}} \bigg] + D_{KL}(q_{\phi}(z|x) || p(z|x)) \tag{15}
\\
&\ge \mathbb{E}_{q_{\phi}(z|x)} \bigg[ log{{p(x,z)} \over {q_{\phi}(z|x)}} \bigg] \tag{16}
\end{align}$$
각 수식을 다시한번 뜯어봅시다.
Eq 9는 확률의 적분은 1과 같으므로 $\int{q_{\phi}(z|x) dz}$를 곱해준 것입니다.
Eq 10은 $log \ p(x)$를 적분 안쪽으로 가져왔습니다.
Eq 11은 기댓값(Expectation)의 공식을 적용하였습니다.
Eq 12는 Eq 2의 $p(x) = {{p(x, z)} \over {p(z|x)}}$를 적용하였습니다.
Eq 13은 ${{q_{\phi}(z|x)} \over {q_{\phi}(z|x)}} = 1$이기 때문에 우변에 값을 곱해주었습니다.
Eq 14는 log를 분리하였습니다.
Eq 15는 KL Divergence로 값을 변환하였습니다.
Eq 16은 KL Divergence는 항상 0 이상이므로 식이 성립합니다.
KL Divergence
KL Divergence는 Kullback-Leibler Divergence(쿨백-라이블러 발산)의 줄임말입니다. 두 확률 분포의 차이를 계산할 때 사용하는 함수로 두 확률 분포에 대한 Cross Entropy를 계산합니다.
$$D_{KL}(P||Q)=\sum_{x \in X}{P(x) log_{b}\bigg({{P(x)} \over {Q(x)}}\bigg)}$$
log의 밑인 b는 정보량을 의미하며 2, 10, e등을 사용합니다.
더 깊게 살펴볼 필요 없이, $\mathbb{E}_{q_{\phi}(z|x)} \bigg[ log{{q_{\phi}(z|x)} \over {p(z|x)}} \bigg] = \int {q_{\phi}(z|x) log{{q_{\phi}(z|x)} \over {p(z|x)}} dz}$ 이므로 KL Divergence로 치환하여 사용하면 $D_{KL}(q_{\phi}(z|x) || p(z|x))$가 됩니다.
자세한 내용은 아래 블로그를 참조하면 됩니다.
https://angeloyeo.github.io/2020/10/27/KL_divergence.html
KL divergence - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
위를 통해 Evidence는 근사확률인 $q_{\phi}(z|x)$ 실제확률인 $p(z|x)$에 대한 ELBO + KL Divergence와 같다는 것을 증명할 수 있습니다.
Variational Autoencoders
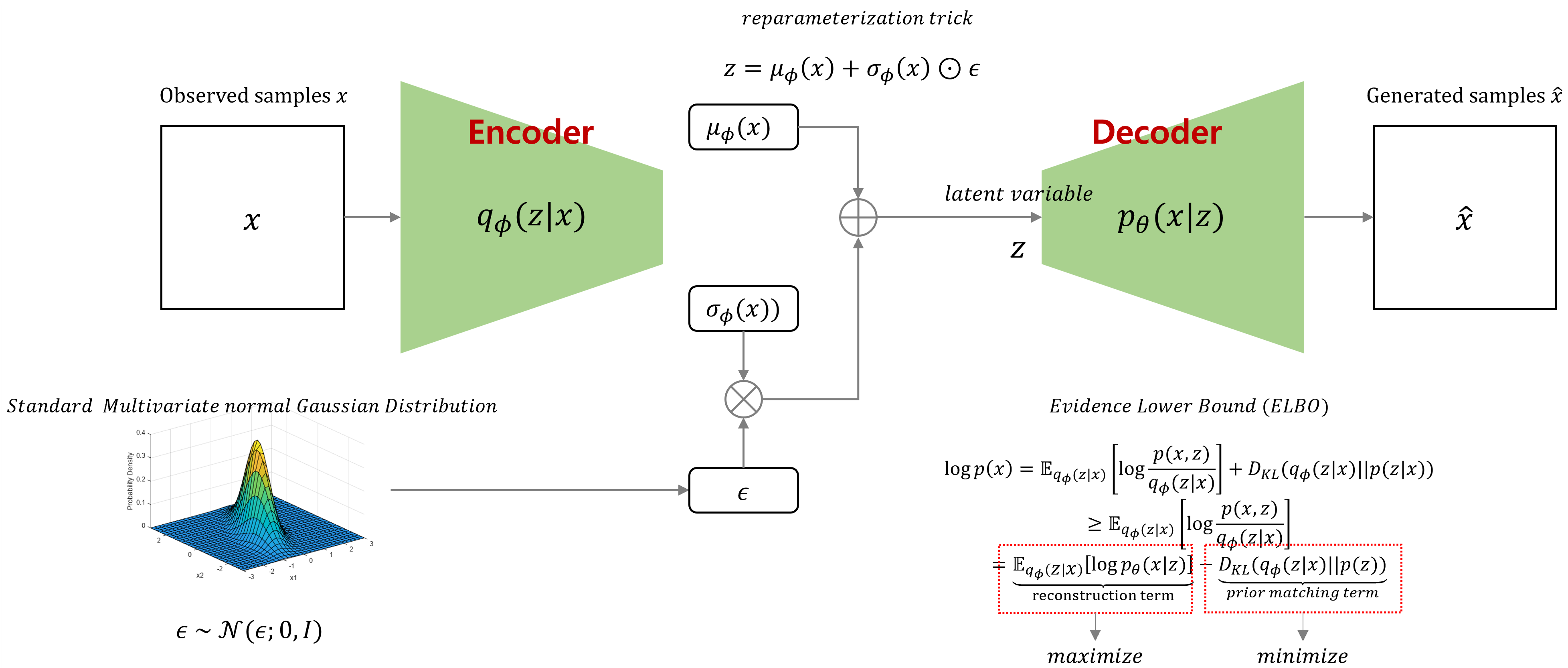
Variational Auto Encoders(VAE)는 기본적으로 ELBO를 maximizing하는 것으로 학습합니다.
$$\begin{align}
\mathbb{E}_{q_{\phi}(z|x)} \bigg[log {{p(x, z)} \over {q_{\phi}(z|x)}} \bigg] & = \mathbb{E}_{q_{\phi}(z|x)} \bigg[log {{p_{\theta}(x|z)p(z)} \over {q_{\phi}(z|x)}} \bigg] \tag{17}
\\
& =\mathbb{E}_{q_{\phi}(z|x)} [log \ p_{\theta}(x|z)] + \mathbb{E}_{q_{\phi}(z|x)} \bigg[ log {{p(z)} \over {q_{\phi}(z|x)}} \bigg] \tag{18}
\\
& =\underbrace{\mathbb{E}_{q_{\phi}(z|x)} [log \ p_{\theta}(x|z)]}_{\rm reconstruction \ term} - \underbrace{D_{KL}(q_{\phi}(z|x) || p(z))}_{\rm prior \ matching \ term} \tag{19}
\end{align}$$
Eq 17은 Probability Chain Rule에 의해 $p(x,z) = p_{\theta}(x|z)p(z)$입니다.
Eq 18은 log 함수에 따라 기댓값을 나눠주었습니다.
이때$\mathbb{E}_{q_{\phi}(z|x)} \bigg[ log {{p(z)} \over {q_{\phi}(z|x)}} \bigg] = \int{q_{\phi}(z|x)\bigg[log {{p(z)} \over {q_{\phi}(z|x)}}\bigg]} dz = -\int{q_{\phi}(z|x)\bigg[log {{q_{\phi}(z|x)} \over {p(z)}}\bigg]} dz =-D_{KL}(q_{\phi}(z|x) || p(z))$을 통해 E19를 도출할 수 있습니다.
수식에서 알 수 있듯 $\mathbb{E}_{q_{\phi}(z|x)} [log \ p_{\theta}(x|z)]$는 Decoder에서 $p_{\theta}(x|z)$를 학습하며 $D_{KL}(q_{\phi}(z|x) || p(z))$는 Encoder에서 bottleneck distribution(병목 분포)인 $q_{\phi}(z|x)$를 학습합니다. KL Divergence를 최소화하고 첫번째 항의 기댓값을 최대화하면 ELBO를 최대화 할 수 있습니다.
VAE의 인코더는 대각 공분산을 갖는 다변량 가우스를 모델링합니다. 기본적으로 다변량 가우스는 표준 다변량 가우스 분포를 사용합니다:
$$q_{\phi}(z|x) = \mathcal{N}(z;\mu_{\phi}(x), \sigma^{2}_{\phi}(x)I) \tag{20}$$
$$p(z) = \mathcal{N}(z;0, I) \tag{21}$$
공분산(covariance)과 공분산 행렬(covariance matrix)
공분산은 2개의 확률변수의 선형관계를 나타내는 값입니다. 쉽게 말해 공분산을 통해 두 확률변수의 상관관계를 파악할 수 있습니다.
공분산 Cov(X, Y)에 대하여 Cov(X, Y)=0일 경우 두 확률변수는 서로 상관관계가 없으며(uncorrelated) Cov(X, Y) > 0 일 때 확률 변수 X의 값이 커질수록 Y의 값도 커지는 관계를 가지고 있습니다. 반대로 Cov(X, Y) < 0일 경우 X의 값이 커질수록 Y 의 값이 작아지는 경향을 보입니다. 공분산은 아래와 같은 수식을 가집니다.
$$Cov(X, Y) = \mathbb{E}\{(X-\mu_{x})(Y-\mu_{y})\}$$
다변량 가우시안 (Multivariate Gaussian)
보통 정규 분포는 하나의 확률 변수 X에 대한 분포를 보여줍니다. 다변량 가우시안 분포는 복수의 확률 변수가 존재할 때 이를 한꺼번에 모델링한 분포입니다. 여러 확률 변수에 대한 각각의 정규분포를 다차원 공간에 확장하여 나타낸 분포입니다.
D 차원의 다변량 정규분포는 평균벡터($\mu$)와 공분산 행렬($\sum$)이라는 두개의 모수를 가지며 다음과 같은 수식으로 정의됩니다.
$$\mathcal{N}(x;\mu,\sum) = {{1} \over {(2\pi)^{D/2}|\sum|^{1/2}}}exp\bigg( -{1 \over 2}(x-\mu)^{T}\sum^{-1}(x-\mu) \bigg)$$
$x$는 확률변수 벡터 $\mu$는 평균 벡터 $\sum$은 공분산 벡터입니다.
또한 일반적으로 평균 $\mu$, 표준편차 $\sigma$를 가진 정규 분포 $\mathcal{N}(x;\mu, \sigma^2)$에 대하여 다음과 같이 정의 할 수 있습니다.
$$\mathcal{N}(x;\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp{(-\frac{(x-\mu)^2}{2\sigma^2})}$$
다음으로는 ELBO의 수식을 몬테 카를로 근사방법(Monte Carlo Approximation)을 통해 근사해봅시다:
$$\underset{\phi, \theta}{arg\ max}{\ \mathbb{E}_{q_{\phi}(z|x)}[log\ p_{\theta}(x|z)] - D_{KL}(q_{\phi}(z|x) || p(z))} \approx \underset{\phi, \theta}{arg\ max}{\ \sum^{L}_{l=1} log\ p_{\theta}(x|z^{(l)}) - D_{KL}(q_{\phi}(z|x) || p(z))} \tag{22}$$
$\{ z^{(l)}\} ^{L}_{l=1}$는 $q_{\phi}(z|x)$의 관측한 x에 대한 latents sample입니다. 이때 z는 확률적으로 샘플링된 값이므로 미분이 불가능합니다. 이것을 $q_{\phi}(z|x)$에 대한 reparameterization trick을 통해 해결합니다.
Monte Carlo Approximation (몬테 카를로 근사방법)
어떤 분포로부터 추출한 Sample에 기반하여 f(X)라는 분포를 근사하는 것을 몬테카를로 적분이라고 합니다. 확률변수의 함수에 대해 기댓값을 근사하는 것은 몬테카를로 근사법이라 합니다. 수식은 다음과 같습니다.
$$E[f(X)] = \int {f(x)p(x) dx} \approx {{1} \over {S}} \sum^{S}_{i=1} f(x_{i})$$
수식을 Eq 21에 적용하면 쉽게 Eq 22를 도출할 수 있습니다. S로 나누는 것은 상수 이기 때문에 따로 쓰지 않은것 같습니다.
Reparameterization trick은 무작위 변수를 deterministic한 함수를 통해 노이즈 변수로 바꿔주는 역할을 합니다. 이를 통해 경사하강을 가능하게 만들어줍니다. 이를 증명해봅시다.
평균 $\mu$, 표준편차 $\sigma$을 갖는 $x \sim \mathcal{N}(x;\mu, \sigma^{2})$의 정규분포는 다음과 같이 나타낼 수 있습니다:
$$x = \mu+\sigma\epsilon \ \rm{with} \ \epsilon \sim \mathcal{N}(\epsilon;0,I)$$
위의 식을 보면 임의의 정규분포 x는 표준 정규분포 $\epsilon$으로 표현할 수 있다는 것을 알 수 있습니다. 평균을 $\mu$만큼 이동하고 분산이 $\sigma^{2}$ 만큼 확장된 표준 정규분포(Standard Gaussian Distribution)으로 해석할 수 있습니다. VAE에서는 각 z는 x와 보조 noise 변수 $\epsilon$ 에 대한 deterministic한 함수로 표현할수 있습니다:
$$z = \mu_{\phi}(x) + \sigma_{\phi}(x) \odot \epsilon \ \rm{with} \ \epsilon \sim \mathcal{N}(\epsilon;0,I)$$
여기서 $\odot$은 element-wise product(Hadamard Product)입니다. 이는 행렬에 대한 원소끼리만 곱한 것을 의미합니다. 즉 Reparameterization trick이란, z를 보조 noise 변수인 $\epsilon$을 사용하여, x에 대한 표준정규분포로 바꾸어 관측된 데이터 x에 대하여 미분 가능하게 만든 것이라고 생각할 수 있습니다. 미분 가능하므로, VAE는 경사하강법을 통해 대한 파라미터인 $\mu$와 $\sigma$를 최적화할 수 있습니다. (즉 ELBO에 대한 추정치를 최적화 합니다.)
따라서 VAE는 잠재공간 p(z)에서 직접 샘플링한 잠재변수를 Decoder를 통해 새로운 데이터를 생성할수 있습니다. VAE에 대한 내용을 토대로 간단하게 Figure를 만들어 봤습니다.
Hierarchical Variational Autoencoders
이번에는 계층적 VAE(HVAE)에 대해 알아봅시다.(생각보다 간단하고 Diffusion과 VAE의 중간 단계정도 되니 간단하게 소개하고 넘어가겠습니다.) HVAE는 VAE보다 더 high-level의 잠재변수를 이끌어 내기 위해 VAE를 계층적으로 쌓아올린 모델입니다. 매우 고차원의 잠재 변수를 VAE를 통해 Decoding 하면 이를 다시 잠재변수로 가정하고 VAE를 Recursion합니다. T개의 계층 레벨이 있다고 할때 HVAE는 다음과 같은 Markov Chain을 가집니다.
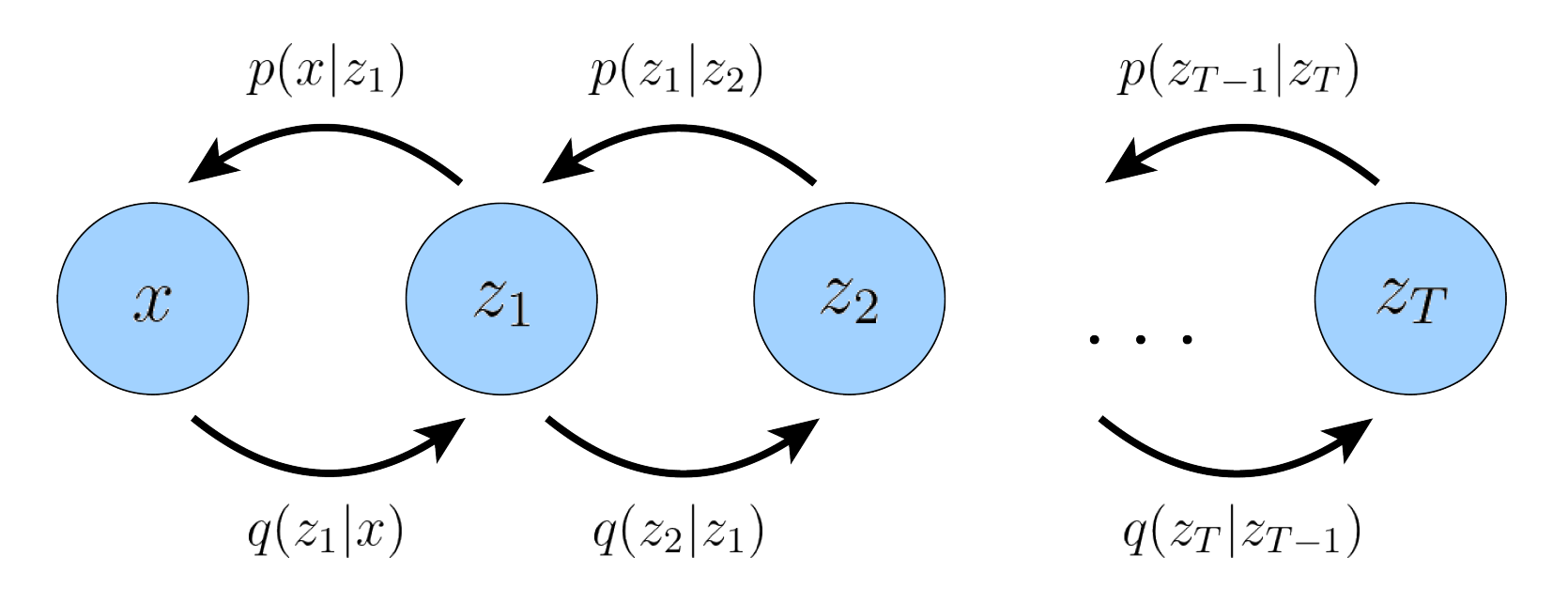
위 그림을 보면 Markov Chain에 대한 수식을 이해하기 쉬워집니다.
$$p(x, z_{1:T}) = p(z_T)p_{\theta}(x|z_{1}) \prod^{T}_{t=2}{p_{\theta}(z_{t-1}|z_{t})} \tag{23}$$
$$q_{\phi}(z_{1:T}|x)=q_{\phi}(z_{1}|x) \prod^{T}_{t=2}{q_{\phi}(z_{t}|z_{t-1})} \tag{24}$$
수식을 통해 ELBO를 도출해봅시다.
$$\begin{align}
\log{p(x)} & = \log{\int{p(x, z_{1:T})dz_{1:T}}} \tag{25}
\\
& = \log{\int{{{p(x, z_{1:T})q_{\phi}(z_{1:T}|x)} \over {q_{\phi}(z_{1:T}|x)}}dz_{1:T}}} \tag{26}
\\
& = \log{\mathbb{E}_{q_{\phi}(z_{1:T}|x)}\bigg[ {{p(x, z_{1:T})} \over {q_{\phi}(z_{1:T}|x)}} \bigg] } \tag{27}
\\
& \ge \mathbb{E}_{q_{\phi}(z_{1:T}|x)}\bigg[ \log {{p(x, z_{1:T})} \over {q_{\phi}(z_{1:T}|x)}} \bigg] \tag{28}
\end{align}$$
Eq 23과 24를 28에 대입하면 최종적으로 다음 식을 얻을 수 있습니다.
$$\mathbb{E}_{q_{\phi}(z_{1:T}|x)}\bigg[ \log{{p(x, z_{1:T})} \over {q_{\phi}(z_{1:T}|x)}}\bigg] = \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \bigg[ \log{{p(z_{T})p_{\theta}(x|z_1)\prod^{T}_{t=2}p_{\theta}(z_{t-1}|z_{t})} \over {q_{\phi}(z_1|x) \prod^{T}_{t=2}q_{\phi}(z_{t}|z_{t-1})}} \bigg] \tag{29}$$
위의 수식은 다음 포스팅에서 나올 Variational Diffusion Models의 기본이 되는 수식입니다. 이번에 공부한 ELBO, VAE, HVAE는 생성모델 중에서도 Diffusion Model(DM)과 매우 밀접한 연관이 있기 때문에 잘 이해하는 것이 중요합니다. 그럼 다음 포스팅에서 뵙겠습니다.
'Generative Models' 카테고리의 다른 글
| [논문 리뷰] Animate Anyone (0) | 2024.03.17 |
|---|---|
| 생성 모델 논문 추천 List - Generative Adversarial Networks (2) | 2023.12.11 |
| [논문 리뷰] Understanding Diffusion Models: A Unified Perspective (3) (0) | 2023.12.11 |
| [논문 리뷰] Understanding Diffusion Models: A Unified Perspective (2) (4) | 2023.08.12 |
| [논문 리뷰] StyTr²: Image Style Transfer with Transformers (0) | 2023.06.07 |
당신이 좋아할만한 콘텐츠
소중한 공감 감사합니다